Some of the terms used and statistics available through CalculateBeta™ are briefly defined and discussed below. For more information, see the Bibliography/Suggested Readings at Where Can I Learn More? Citations herein (in author-year format) refer to sources listed there. If you are not familiar with the Capital Asset Pricing Model (CAPM) you may want to read the Cost of Equity section first.
- Beta
- R-Squared
- Standard Error of Beta
- t-Statistic
- Unlevered Beta
- Data Used to Unlever Betas
- Smoothed Betas
- Sum Beta
- Total Beta
- Equity Risk Premium
- Company-Specific Risk and Size Premiums
- Cost of Equity
This is the “raw” beta, which may be calculated by regressing a stock’s returns against the market’s returns. CalculateBeta uses total returns for both, which results in improved beta estimates, for dividend-paying companies in particular. The stock’s beta is the slope of the resulting ordinary least squares (OLS) regression line. Beta may also be calculated as the covariance of the stock’s returns with the market’s returns, divided by the variance of the market’s returns, i.e., as:
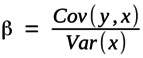
where y represents a series of stock returns and x represents a series of market returns.1 The formulas for covariance and variance are, respectively:

and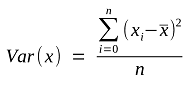
where yi and xi represent an individual stock’s returns and the market’s returns, respectively, and ȳ and x̄ represent the mean average stock and market returns, over n periods.
Beta measures the sensitivity of a stock’s returns to the market’s returns. In the capital asset pricing model (CAPM), beta is a measure of “systematic” risk.
Systematic risk refers to risks that affect all assets to some degree, and which therefore cannot be diversified away. As a measure of systematic risk, beta does not include that portion of an individual stock’s risk which is unique or specific to the individual stock. Such risk is “unsystematic”, and can be eliminated through diversification.
The risk of a rise in interest rates is an example of a systematic risk. The risk of an earthquake destroying inventory because a company’s warehouse was built on a fault line is an unsystematic risk. Unsystematic risk is not captured in beta. Modern portfolio theory holds that unsystematic risks are generally not priced in stock (and other asset) markets because buyers and sellers can eliminate such risks by holding diversified portfolios.
The raw beta is also referred to as the “levered” beta. Levered betas are called “levered” because observed stock price movements reflect companies’ financial leverage as well as their operating characteristics. There are ways to adjust for the effects of financial leverage on beta (see below).
In the linear regression model used to estimate betas, R-squared may be computed as one minus the average of the squared differences between actual stock returns and the predicted stock returns (i.e., the variance of the model residuals), divided by the variance in the actual stock returns, or:

where yi represents the stock's actual returns, ŷi represents the returns predicted by the regression, and ȳ represents the mean average stock return, over n periods.
Intuitively, the variance of the model residuals as a fraction of the variance of the actual stock returns can be thought of as the percentage of the variance of the actual stock returns which is “left over”, or not explained, by the market’s returns. Therefore, 1 minus this amount can be thought of as the percentage of the variance of the stock returns which is explained by the market’s returns.
R-squared varies between 0 and 1. A beta estimate with a high R-squared indicates that most of that stock’s variability of returns is explained by the market’s varying returns. For example, an R-squared of 0.7 indicates that 70% of the stock's returns are explained by the market's returns. Most of such a stock’s total risk is systematic risk, or market risk. The reverse is true for a beta estimate with a low R-squared. Most individual stock betas have a low R-squared. This is consistent with portfolio theory and the CAPM.
The formula above gives the “unadjusted” R-squared. It may overstate the strength of relationship between the independent and dependent variables if the number of observations is not much larger than the number of parameters in the regression model. “Adjusted R-squared” adjusts for the number of independent variables p (p = 1 in the case of the simple linear regression model used to estimate beta). Since there is only one independent variable used in estimating betas, and CalculateBeta typically uses at least 30 return observations in its calculations, unadjusted R-squared and adjusted R-squared will usually be close.
The formula for adjusted R-squared is:

The standard error of beta is an estimate of the standard deviation of the sampling distribution of the beta. It indicates the extent to which a company’s true beta may differ from its estimated beta.
For example, if a beta of 1.20 has a standard error of 0.15, then there is an approximately 68% chance that the true beta for this stock lies between 1.05 and 1.35, and an approximately 95% chance that it lies between 0.90 and 1.50.2
Dr. Aswath Damodaran of New York University’s Stern School of Business has noted that the quality of an average peer group or industry beta is better than that of the individual betas making up the industry or peer group. “Averaging across these betas results in an average beta that is far more precise than the individual betas that went into it. In fact, if the estimation errors on individual betas are uncorrelated across firms, the savings in standard error can be stated as a function of the average standard error ... and the number of firms in the sample.” (Damodaran 2012, page 198) Specifically, he notes that the standard error of the average beta will equal the average of the standard errors of the individual guideline company betas, divided by the square root of the number of guideline companies. A similar observation is made by McKinsey, et al. (2015). As the number of guideline companies increases, the reduction in standard error can become substantial.3
This figure is provided by CalculateBeta as the "Standard Error of Average Beta" on the "Beta Calculations" tab in subscribers' beta cases.
In the case of betas calculated using CalculateBeta the provided t-statistic is the estimated raw (levered) beta divided by the standard error of the beta.
If beta is large relative to its standard error, you will have a high t-statistic, indicating a relatively high level of confidence that beta is not zero, and a relatively tight range around the estimate of beta. The specific confidence level indicated by a given t-statistic is dependent on the number of degrees of freedom in the calculation. Since CalculateBeta will not allow you to request fewer than 30 returns, the minimum number of degrees of freedom in a regression performed by CalculateBeta will normally be 28. With 28 degrees of freedom, a t-statistic of 1.70 provides a confidence level of approximately 90% that beta is not zero. A t-statistic of 2.05 provides a confidence level of approximately 95% that beta is not zero. The t-statistics required for these levels of confidence decrease as the number of observations increases, approaching those associated with the normal distribution (which are 1.65 and 1.96, respectively - i.e., 28 degrees of freedom is already pretty close to normal, for this purpose).
The raw betas computed from regressing stock returns against market returns reflect the risk of both the underlying company’s operating characteristics and its financial structure. A company’s use of debt adds additional risk for stockholders, since the residual cash flows left over for equity become more volatile due to the relatively fixed cash flow obligations created by borrowing.
Different companies have different capital structures, and the same company may have different capital structures at different times. In order to meaningfully use betas, analysts must often remove the effects of financial leverage from the beta estimate. Such "unlevered" betas will be lower than (or, in the case of all-equity financed firms, equal to) the levered betas from which they are calculated.
CalculateBeta retrieves fundamental financial data about companies as of their most recent balance sheet date (i.e., the most recent quarter preceding the “as-of” date you specify), and uses that data to unlever the raw betas. CalculateBeta uses the Hamada (1971) formula to unlever betas. For more information about the financial data used to unlever betas, see Data Used to Unlever Betas, below.
The Hamada formulas were introduced in the 1970s and remain the most commonly used formulas for unlevering and relevering betas.4 They state that unlevered beta equals levered beta divided by 1 plus the company’s tax-adjusted debt-to-equity ratio, or:
where,
ßu = the unlevered beta
ßl = the levered beta
t = the marginal tax rate
D = the market value of the firm’s debt
E = the market value of the firm’s equity
Conversely, unlevered betas can be relevered using the following formula:
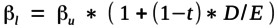
These formulas can be used to unlever the betas of a selected peer group of guideline companies, providing a set of beta estimates reflecting a similar amount of leverage (i.e., with all companies in the peer group financed entirely with equity). In valuation analysis, this provides a basis for selecting an unlevered beta, which is then relevered to a subject company's actual or target capital structure.
For most non-financial stocks, CalculateBeta calculates a company’s valuation date debt-to-equity ratio and trailing twelve months effective tax rate, which are then used to unlever the company's raw, levered, ordinary least squares beta. (For financial sector stocks, including insurance and real estate, CalculateBeta provides levered betas and other detailed data, but because of the unique characteristics of these firms' balance sheets, does not calculate debt-to-equity ratios or unlevered betas. CalculateBeta also does not calculate these items for a small number of other securities, such as American Depositary Receipts).
FactSet, the source of the balance sheet and income statement data used by CalculateBeta, provides the following information regarding the financial statement items used to calculate debt-to-equity ratios and effective tax rates:
Short-Term Debt
Represents that portion of debt payable within one year including current portion of long-term debt and sinking fund requirements of preferred stock or debentures.
Long-Term Debt
Represents all interest-bearing financial obligations, excluding amounts due within one year. It is shown net of premium or discount.
Preferred Stock (Book Value)
Represents a claim prior to the common shareholders on the earnings of a company and on the assets in the event of liquidation.
Income Taxes
Represents all income taxes levied on the income of a company by federal, state and foreign governments.
Pre-tax Income
Represents all income/loss before any federal, state or local taxes. Extraordinary items reported net of taxes are excluded.
The market value of common equity is calculated using the most recent available shares outstanding preceding the "as-of" date multiplied by the "as-of" date closing price of the stock, both adjusted for splits.5 The book value of preferred stock, if any, is included in debt in calculating the debt-to-equity ratio (when preferred stock is present, you may wish to evaluate its terms to see if this treatment merits adjustment).
The effective tax rate is determined for calculation purposes as the ratio of income taxes over pre-tax income. If the tax rate so determined falls outside of the range of 10% to 50%, a tax rate of 35% is assumed. (Tax rates are easily adjusted in worksheets downloaded from CalculateBeta, if your preferences are different).
Studies beginning with Blume (1971) and others indicate that betas tend to regress to the mean over time. CalculateBeta does not calculate a smoothed beta, but one common and simple procedure is to multiply the raw (levered) beta by 67%, multiply 1.0 by 33%, and add the two products together. Bloomberg and others “smooth” beta in this or a similar fashion.
More refined techniques for adjusting betas exist and are discussed in finance literature. There are techniques which consider a tendency to regress to an industry or peer group beta rather than to a market beta of 1.0, and/or to place more weight on companies’ raw regression betas when the standard error of a regression beta is relatively low, and more weight on an industry or market beta when a company’s regression beta has a relatively high standard error. See, e.g., Duff & Phelps / Grabowksi, et al. (2017) and McKinsey, et al. (2015).
In general, regression betas are less likely to need smoothing or other adjustment when their standard errors are low. As noted above regarding the Standard Error of Beta, when using a well-defined group of companies as a peer group or industry the average beta will often have a low standard error.
Sum beta attempts to account for the fact that because the stocks of smaller companies are less followed and less traded, their prices may react to market movements with a lag ("non-synchronous" trading). Therefore, the calculation of sum beta considers the prior period return of the selected market index as well as the current period return. One way to compute sum betas is to perform a regression with the stock return as the dependent variable, both the current and the lagged index returns as independent variables, and then "sum" the coefficients of the two independent variables (see, e.g., Ibbotson 1997). The current and lagged coefficients can also be computed algebraically (see, e.g., Pratt and Grabowski, 2014). To the best of our knowledge, at this writing CalculateBeta is the only service which calculates and provides sum betas.
The equity risk premium represents the additional return expected on an investment in equities over a risk-free asset, such as U. S. Treasury bonds. The equity risk premium can be estimated in several ways, including, for example, i) historical experience (i.e., the average return stocks earned in excess of the return on Treasury bonds over past periods), ii) current market conditions, as implied using a variation of the dividend discount or Gordon growth model (see, e.g., Damodaran 2012), or iii) surveys of capital market participants.
Average historical equity risk premiums are most widely relied on for guidance regarding future expected equity risk premiums. Average historical premiums can be calculated in various ways, depending on the historical time period considered, the selection of the market index and the risk-free asset, and whether averaging is performed on an arithmetic or geometric basis. Calculate Beta provides the ability to calculate historical equity risk premiums in a variety of ways.
Company-Specific Risk and Size Premiums
- CalculateBeta calculates unlevered betas for each of the public peer group companies, computes their median unlevered beta, and relevers it using the median effective tax rate and debt-to-equity ratio of your chosen public company peer group.
- CalculateBeta retrieves and uses as the risk-free rate the "as of" date interest rate for 10-year Treasury securities as per the Federal Reserve.
- CalculateBeta calculates and uses an estimate of the market equity risk premium, based on the arithmetic average of the annual S&P 500 total return in excess of the 10-year Treasury income return, calculated using the month-end preceding your specified valuation date as the ending point, and the first such month-end following April of 1954 as the beginning point.
To clarify by example: If you specify a valuation date of November 15, 2016, CalculateBeta will, by default, automatically retrieve and use the 10-year constant maturity Treasury rate as of that date (2.23%), and calculate and use an equity risk premium based on the arithmetic average of the 62 annual returns for annual periods ending at the end of October 1954 through October 2016 (6.02%). This risk-free rate and market equity premium will be used, along with your peer group's relevered median beta, to calculate a peer group CAPM cost of equity as of your given date.
A note on mechanics: Subscribers can, if desired, easily download spreadsheets for their beta and cost of equity cases and substitute alternative data for the defaults used by CalculateBeta. CalculateBeta's tools provide some alternative risk-free rate and equity risk premium information you may wish to consider in place of its defaults, and you can also easily substitute data from other sources.
1 Performing this computation with excess total returns - that is, with total stock and market returns in excess of the risk-free rate - is theoretically preferable. However, many sources of betas calculate beta using total returns because, in practice, it makes little difference to the results obtained. CalculateBeta uses total returns.
2 These probabilities assume a normal distribution. If you wish to establish a more precise confidence interval for a company's beta, use a t distribution with n - 2 degrees of freedom, where n is the number of observations (returns) used to compute beta. The t distribution approximates the normal distribution as the number of observations increases. Since CalculateBeta requires that you request at least 30 periods, the applicable t distribution for betas calculated using CalculateBeta will typically not stray far from a normal distribution.
3 Prof. Damodaran (2012) and others (for example, McKinsey, et al., 2015) recommend considering such industry or peer group mean and median betas to value individual public companies, when possible, rather than an individual company's own regression beta, to improve the quality of the estimate through this reduction in standard error. When the subject company is private, of course, it has no regression beta of its own.
When a subject company is in multiple lines of business, these authors recommend using a weighted average of applicable industry / peer group betas, weighted by the subject company's sales (or profits) in each industry or line of business, to determine a weighted average or (Dr. Damodaran's term) "bottom-up" beta.
4 The Hamada formulas are widely used in practice. However, there are alternatives (see, e.g., Harris and Pringle, 1985), which may be more appropriate in some circumstances. Pratt and Grabowski (2014) provide an interesting discussion of alternative formulas for unlevering and relevering betas. See also Hitchner (2017). The main drawback of these alternatives is that they require the use of betas for firms' debt which, practically, must often be assumed.
While the Hamada formulas refer to the market value of debt, the book value of debt is typically used for both unlevering and relevering, rather than the market value. Unlike equity, the book and market values of debt are typically close. CalculateBeta uses the book value of debt in these calculations.5 Please note: only for splits. These prices may therefore differ from prices as of the same date which CalculateBeta uses to calculate total returns and betas, since the latter are adjusted for both splits and dividends. We make this distinction because, when computing market capitalization, it may be important to exclude the effect of dividends paid after the "as-of" date.
